A Mass Is Accelerated When

Rate of change of velocity

Acceleration
In vacuum (no air resistance), objects attracted by Earth gain speed at a steady rate.
Common symbols	a
SI unit	thou/s^two, k·due south^−two, 1000 s^−two
Derivations from other quantities	$\mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d^{two}\mathbf {x} }{dt^{2}}}$
Dimension	${\mathsf {Fifty}}{\mathsf {T}}^{-2}$

In mechanics, dispatch is the rate of modify of the velocity of an object with respect to time. Accelerations are vector quantities (in that they have magnitude and direction).^[1] ^[two] The orientation of an object'southward dispatch is given past the orientation of the internet strength acting on that object. The magnitude of an object'south acceleration, as described by Newton's Second Police,^[3] is the combined effect of two causes:

the net balance of all external forces interim onto that object — magnitude is directly proportional to this net resulting force;
that object's mass, depending on the materials out of which it is made — magnitude is inversely proportional to the object's mass.

The SI unit for dispatch is metre per second squared (m⋅s⁻ⁱⁱ , $\mathrm {\tfrac {thousand}{south^{ii}}}$ ).

For example, when a vehicle starts from a standstill (zero velocity, in an inertial frame of reference) and travels in a straight line at increasing speeds, it is accelerating in the direction of travel. If the vehicle turns, an acceleration occurs toward the new direction and changes its move vector. The acceleration of the vehicle in its electric current direction of move is called a linear (or tangential during round motions) acceleration, the reaction to which the passengers on board feel as a forcefulness pushing them dorsum into their seats. When changing direction, the effecting dispatch is called radial (or centripetal during round motions) acceleration, the reaction to which the passengers feel as a centrifugal forcefulness. If the speed of the vehicle decreases, this is an dispatch in the opposite direction and mathematically a negative, sometimes called deceleration or retardation, and passengers feel the reaction to deceleration as an inertial strength pushing them forward. Such negative accelerations are frequently achieved by retrorocket called-for in spacecraft.^[4] Both acceleration and deceleration are treated the aforementioned, every bit they are both changes in velocity. Each of these accelerations (tangential, radial, deceleration) is felt past passengers until their relative (differential) velocity are neutralized in reference to the acceleration due to change in speed.

Definition and properties [edit]

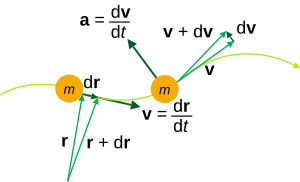
Kinematic quantities of a classical particle: mass $m$ , position $r$ , velocity $5$ , dispatch $a$ .

Average acceleration [edit]

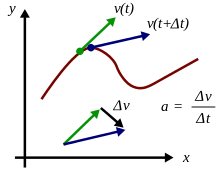
Acceleration is the charge per unit of change of velocity. At any point on a trajectory, the magnitude of the acceleration is given by the rate of alter of velocity in both magnitude and direction at that point. The true acceleration at time $t$ is found in the limit every bit time interval $Δ t \to 0$ of $Δ 5 /Δ t$

An object's average acceleration over a flow of time is its change in velocity, $\Delta \mathbf {v}$ , divided by the duration of the period, $\Delta t$ . Mathematically,

{\bar {\mathbf {a} }}={\frac {\Delta \mathbf {five} }{\Delta t}}.

Instantaneous dispatch [edit]

From bottom to top:

an acceleration role $a (t)$ ;
the integral of the dispatch is the velocity function $five (t)$ ;
and the integral of the velocity is the distance function $s (t)$ .

Instantaneous acceleration, meanwhile, is the limit of the average acceleration over an infinitesimal interval of fourth dimension. In the terms of calculus, instantaneous acceleration is the derivative of the velocity vector with respect to time:

\mathbf {a} =\lim _{{\Delta t}\to 0}{\frac {\Delta \mathbf {v} }{\Delta t}}={\frac {d\mathbf {v} }{dt}}

As acceleration is defined as the derivative of velocity, $v$ , with respect to fourth dimension $t$ and velocity is defined as the derivative of position, $x$ , with respect to time, acceleration tin be thought of as the 2d derivative of $10$ with respect to $t$ :

\mathbf {a} ={\frac {d\mathbf {five} }{dt}}={\frac {d^{ii}\mathbf {x} }{dt^{ii}}}

(Here and elsewhere, if motion is in a straight line, vector quantities tin exist substituted past scalars in the equations.)

By the cardinal theorem of calculus, information technology can be seen that the integral of the acceleration role $a (t)$ is the velocity role $5 (t)$ ; that is, the area under the curve of an acceleration vs. time ( $a$ vs. $t$ ) graph corresponds to the change of velocity.

As well, the integral of the jerk function $j (t)$ , the derivative of the acceleration function, tin be used to find the change of acceleration at a sure time:

\mathbf {\Delta a} =\int \mathbf {j} \,dt

Units [edit]

Dispatch has the dimensions of velocity (L/T) divided by time, i.e. L T^−two. The SI unit of acceleration is the metre per 2d squared (grand s⁻²); or "metre per second per second", as the velocity in metres per 2nd changes by the dispatch value, every second.

Other forms [edit]

An object moving in a circular motion—such every bit a satellite orbiting the Earth—is accelerating due to the change of direction of motion, although its speed may be abiding. In this example it is said to be undergoing centripetal (directed towards the center) acceleration.

Proper dispatch, the acceleration of a trunk relative to a free-fall condition, is measured by an instrument chosen an accelerometer.

In classical mechanics, for a body with constant mass, the (vector) acceleration of the body's center of mass is proportional to the net force vector (i.e. sum of all forces) acting on information technology (Newton'south second law):

where $F$ is the internet force interim on the body, $m$ is the mass of the torso, and $a$ is the center-of-mass acceleration. As speeds approach the speed of calorie-free, relativistic effects get increasingly large.

Tangential and centripetal dispatch [edit]

An oscillating pendulum, with velocity and acceleration marked. It experiences both tangential and centripetal acceleration.

Components of dispatch for a curved motility. The tangential component $a t$ is due to the change in speed of traversal, and points along the curve in the management of the velocity vector (or in the opposite direction). The normal component (as well chosen centripetal component for circular motion) $a c$ is due to the change in direction of the velocity vector and is normal to the trajectory, pointing toward the heart of curvature of the path.

The velocity of a particle moving on a curved path as a part of time can be written as:

\mathbf {v} (t)=five(t){\frac {\mathbf {v} (t)}{v(t)}}=v(t)\mathbf {u} _{\mathrm {t} }(t),

with $v (t)$ equal to the speed of travel along the path, and

\mathbf {u} _{\mathrm {t} }={\frac {\mathbf {5} (t)}{v(t)}}\,,

a unit of measurement vector tangent to the path pointing in the direction of motion at the chosen moment in time. Taking into account both the irresolute speed $v (t)$ and the irresolute direction of $u t$ , the acceleration of a particle moving on a curved path tin be written using the chain rule of differentiation^[5] for the product of two functions of time as:

{\brainstorm{alignedat}{3}\mathbf {a} &={\frac {d\mathbf {v} }{dt}}\\&={\frac {dv}{dt}}\mathbf {u} _{\mathrm {t} }+v(t){\frac {d\mathbf {u} _{\mathrm {t} }}{dt}}\\&={\frac {dv}{dt}}\mathbf {u} _{\mathrm {t} }+{\frac {v^{ii}}{r}}\mathbf {u} _{\mathrm {north} }\ ,\end{alignedat}}

where $u n$ is the unit (inward) normal vector to the particle'south trajectory (also chosen the principal normal), and $r$ is its instantaneous radius of curvature based upon the osculating circumvolve at fourth dimension $t$ . These components are chosen the tangential acceleration and the normal or radial dispatch (or centripetal acceleration in circular motion, run into also circular movement and centripetal forcefulness).

Geometrical analysis of three-dimensional infinite curves, which explains tangent, (principal) normal and binormal, is described by the Frenet–Serret formulas.^[vi] ^[7]

Special cases [edit]

Compatible acceleration [edit]

Calculation of the speed departure for a compatible acceleration

Uniform or abiding acceleration is a type of motion in which the velocity of an object changes by an equal amount in every equal time period.

A frequently cited instance of uniform acceleration is that of an object in free fall in a uniform gravitational field. The acceleration of a falling trunk in the absence of resistances to motion is dependent just on the gravitational field strength $g$ (also called acceleration due to gravity). By Newton'southward Second Law the forcefulness $\mathbf {F_{thousand}}$ interim on a torso is given by:

\mathbf {F_{g}} =m\mathbf {g}

Considering of the unproblematic analytic properties of the case of constant acceleration, there are uncomplicated formulas relating the deportation, initial and time-dependent velocities, and acceleration to the fourth dimension elapsed:^[8]

{\begin{aligned}\mathbf {s} (t)&=\mathbf {s} _{0}+\mathbf {five} _{0}t+{\tfrac {ane}{2}}\mathbf {a} t^{ii}=\mathbf {s} _{0}+{\tfrac {1}{2}}\left(\mathbf {v} _{0}+\mathbf {v} (t)\right)t\\\mathbf {five} (t)&=\mathbf {v} _{0}+\mathbf {a} t\\{v^{2}}(t)&={v_{0}}^{2}+2\mathbf {a\cdot } [\mathbf {south} (t)-\mathbf {southward} _{0}]\end{aligned}}

where

In particular, the motion can be resolved into ii orthogonal parts, one of constant velocity and the other according to the to a higher place equations. As Galileo showed, the net effect is parabolic motion, which describes, e. k., the trajectory of a projectile in a vacuum well-nigh the surface of Earth.^[9]

Circular motion [edit]

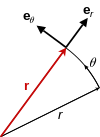
Position vector r, always points radially from the origin.

Velocity vector v, always tangent to the path of motility.

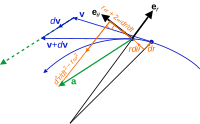
Acceleration vector a, not parallel to the radial motion merely get-go by the angular and Coriolis accelerations, nor tangent to the path merely outset past the centripetal and radial accelerations.

Kinematic vectors in plane polar coordinates. Observe the setup is not restricted to 2nd space, but may represent the osculating plane plane in a point of an arbitrary curve in any higher dimension.

In uniform round motion, that is moving with constant speed along a circular path, a particle experiences an acceleration resulting from the change of the direction of the velocity vector, while its magnitude remains constant. The derivative of the location of a indicate on a bend with respect to fourth dimension, i.east. its velocity, turns out to exist always exactly tangential to the curve, respectively orthogonal to the radius in this betoken. Since in compatible movement the velocity in the tangential direction does not change, the acceleration must be in radial direction, pointing to the center of the circle. This dispatch constantly changes the management of the velocity to be tangent in the neighboring point, thereby rotating the velocity vector forth the circle.

Expressing centripetal acceleration vector in polar components, where $\mathbf {r}$ is a vector from the eye of the circle to the particle with magnitude equal to this distance, and considering the orientation of the acceleration towards the center, yields

\mathbf {a_{c}} =-{\frac {v^{two}}{|\mathbf {r} |}}\cdot {\frac {\mathbf {r} }{|\mathbf {r} |}}\,.

As usual in rotations, the speed $v$ of a particle may exist expressed every bit an angular speed with respect to a point at the distance $r$ equally

Thus $\mathbf {a_{c}} =-\omega ^{2}\mathbf {r} \,.$

This acceleration and the mass of the particle make up one's mind the necessary centripetal strength, directed toward the center of the circle, equally the net force acting on this particle to keep it in this uniform circular motion. The so-called 'centrifugal force', appearing to act outward on the body, is a so-called pseudo force experienced in the frame of reference of the body in circular motion, due to the torso'due south linear momentum, a vector tangent to the circle of motion.

In a nonuniform circular motion, i.due east., the speed along the curved path is irresolute, the dispatch has a non-zero component tangential to the curve, and is non bars to the master normal, which directs to the heart of the osculating circle, that determines the radius $r$ for the centripetal acceleration. The tangential component is given by the angular acceleration $\alpha$ , i.e., the charge per unit of change $\alpha ={\dot {\omega }}$ of the angular speed $\omega$ times the radius $r$ . That is,

a_{t}=r\alpha .

The sign of the tangential component of the acceleration is determined by the sign of the athwart acceleration ( $\alpha$ ), and the tangent is always directed at right angles to the radius vector.

Relation to relativity [edit]

Special relativity [edit]

The special theory of relativity describes the behavior of objects traveling relative to other objects at speeds budgeted that of light in a vacuum. Newtonian mechanics is exactly revealed to exist an approximation to reality, valid to peachy accurateness at lower speeds. As the relevant speeds increase toward the speed of light, acceleration no longer follows classical equations.

Every bit speeds approach that of light, the acceleration produced by a given force decreases, becoming infinitesimally small as light speed is approached; an object with mass can arroyo this speed asymptotically, simply never reach information technology.

General relativity [edit]

Unless the state of motility of an object is known, it is incommunicable to distinguish whether an observed force is due to gravity or to acceleration—gravity and inertial acceleration take identical effects. Albert Einstein called this the equivalence principle, and said that only observers who experience no force at all—including the forcefulness of gravity—are justified in concluding that they are not accelerating.^[x]

Conversions [edit]

Conversions between common units of dispatch
Base value	(Gal, or cm/s²)	(ft/s²)	(grand/sⁱⁱ)	(Standard gravity, g ₀)
1 Gal, or cm/southwardⁱⁱ	i	0.0328084	0.01	1.01972 ×10⁻³
1 ft/s²	30.4800	i	0.304800	0.0310810
ane k/s²	100	three.28084	i	0.101972
1 grand ₀	980.665	32.1740	nine.80665	one

References [edit]

^ Bondi, Hermann (1980). Relativity and Common Sense. Courier Dover Publications. pp. three. ISBN978-0-486-24021-iii.
^ Lehrman, Robert L. (1998). Physics the Piece of cake Manner. Barron's Educational Series. pp. 27. ISBN978-0-7641-0236-3.
^ Crew, Henry (2008). The Principles of Mechanics. BiblioBazaar, LLC. p. 43. ISBN978-0-559-36871-4.
^ Raymond A. Serway; Chris Vuille; Jerry Southward. Faughn (2008). Higher Physics, Volume 10. Cengage. p. 32. ISBN9780495386933.
^ Weisstein, Eric W. "Chain Rule". Wolfram MathWorld. Wolfram Research. Retrieved ii August 2016.
^ Larry C. Andrews; Ronald L. Phillips (2003). Mathematical Techniques for Engineers and Scientists. SPIE Printing. p. 164. ISBN978-0-8194-4506-three.
^ Ch V Ramana Murthy; NC Srinivas (2001). Applied Mathematics. New Delhi: S. Chand & Co. p. 337. ISBN978-81-219-2082-7.
^ Keith Johnson (2001). Physics for you: revised national curriculum edition for GCSE (4th ed.). Nelson Thornes. p. 135. ISBN978-0-7487-6236-1.
^ David C. Cassidy; Gerald James Holton; F. James Rutherford (2002). Agreement physics. Birkhäuser. p. 146. ISBN978-0-387-98756-9.
^ Brian Greene, The Fabric of the Creation: Space, Time, and the Texture of Reality, folio 67. Vintage ISBN 0-375-72720-v

External links [edit]

Dispatch Calculator Simple dispatch unit converter
Acceleration Calculator Acceleration Conversion calculator converts units grade meter per second square, kilometer per 2d square, millimeter per second square & more with metric conversion.